Answer:
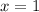 and
and
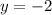 .
.
Explanation:
We have been given a system of equations. We are asked to simplify our given system by the elimination method.
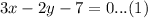
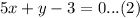
First of all, we will multiply equation (2) by 2 as shown below:

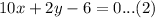
Upon adding equation (1) and (2), we will get:

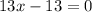
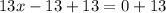
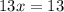
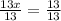
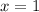
Upon substituting
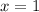 in equation (2), we will get:
in equation (2), we will get:

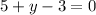
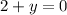
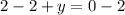
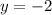
Therefore, the solution for our given system of equation is
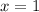 and
and
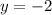 .
.