Question

What is the equation of the parabola with a vertex at (-2, 3) and a focus at (-2, 0)? Does it open upward or downward?

a.
(x + 2)883-12-01-00-00_files/i0060000.jpg = 0.4(y - 3); upward
c.
(x + 2)883-12-01-00-00_files/i0060001.jpg = -12(y - 3); downward
b.
(x + 2)883-12-01-00-00_files/i0060002.jpg = 8(y - 3); upward
d.
(x + 2)883-12-01-00-00_files/i0060003.jpg = -8(y - 3); downward

Answer 1

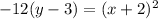`-12(y-3)=(x+2)^2` , downward

Explanation:

Given : (h,k) = vertex location = (-2, 3)

Focus = (-2, 0)

This the downward parabola because the vertex is above the focus.

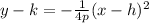`y-k= -(1)/(4p)(x-h)^2` -----1

where(h,k)is the vertex

p is distance vertex to focus

To Find Distance between focus and vertex we will use distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`(x_1,y_1)=(-2,3)`

`(x_2,y_2)=(-2,0)`

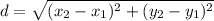
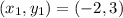
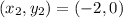
Substitute the values

`d=√((-2+2)^2+(0-3)^2)`

`d=√(3^2)`

`d=3`

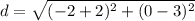
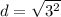
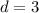
So, value of p = 3

Now substitute the values in 1

`y-3=(1)/(4(3))(x+2)^2`

`y-3=(1)/(12)(x+2)^2`

`y-3=-(1)/(12)(x+2)^2`

`-12(y-3)=(x+2)^2`

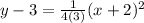
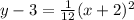
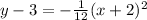
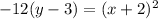
Thus the equation of the parabola is
`-12(y-3)=(x+2)^2`

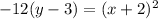
Thus Option C is correct:
`-12(y-3)=(x+2)^2` , downward

Answer 2

Refer to the diagram shown below.

The distance, d, from the focus to a point P (x,y) is equal to the distance from the directrix to P.
Therefore
d² = (6 - y)²
= (x + 2)² + y²
That is,
36 - 12y + y² = (x + 2)² + y²
12y = -(x + 2)² + 36

The equation of the parabola is
y = -(1/12)(x + 2)² + 3
It may be written as
-12(y - 3) = (x + 2)²

The leading coefficient -1/12 is negative, therefore the curve opens downward.

Answer:
The equation is (x + 2)² = -12(y - 3).
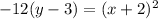The curve opens downward.