Solution:
Product of two rational numbers always Rational:
As given
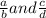 are two rational numbers.
are two rational numbers.
So, all a,b,c,d are integers such that b ≠ 0, and d≠ 0.
So the product of
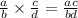 such that bd≠ 0.→→[Integers are closed under multilication i.e follows commutative property under multiplication]
such that bd≠ 0.→→[Integers are closed under multilication i.e follows commutative property under multiplication]
→ Which shows that
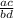 is rational number.
is rational number.