Question

A box contains 24 transistors,4 of which are defective. If 4 are sold at random,find the following probabilities. i. Exactly 2 are defectiveii.None is defectiveiii All are defective iv. At least one is defective

Answer 1

This is a binomial probability. For i, we will apply the Binomial probability formula

i. Exactly 2 are defective

Using the formula, we have

`\begin{gathered} P_x=^nC_x\left(p^x\right?\left(q^(n-x)\right) \\ Where\text{ } \\ P_x=binomial\text{ probability} \\ x=number\text{ of times for a specific outcome with n trials =2} \\ p=\text{ probability of success = }(4)/(24)=(1)/(6) \\ q=probability\text{ of failure =1-}(1)/(6)=(5)/(6) \\ ^nC_x=\text{ number of combinations = }^4C_2 \\ n=\text{ number of trials = 4} \end{gathered}`

Note that I made the probability of being defective as the probability of success = p

and probability of none defective as probability of failure = q

Exactly 2 are defective becomes the binomial probability

`\begin{gathered} P_x=^4C_2*\lparen(1)/(6))^2*\lparen(5)/(6))^(4-2) \\ P_x=6*(1)/(36)*(25)/(36) \\ P_x=(25)/(216) \\ =0.1157 \end{gathered}`

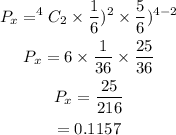
Hence the answer is 0.1157

(ii) None is defective becomes

`\begin{gathered} \lparen(5)/(6))^4=(625)/(1296) \\ =0.4823 \end{gathered}`

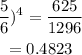
hence the answer is 0.4823

(iii) All are defective

`\begin{gathered} \lparen(1)/(6))^4=(1)/(1296) \\ =0.00077 \end{gathered}`

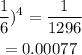
(iv) At least one is defective

This is 1 - probability that none is defective

`\begin{gathered} 1-\lparen(5)/(6))^4 \\ =1-(625)/(1296) \\ =(671)/(1296) \\ =0.5177 \end{gathered}`

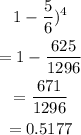
Hence the answer is 0.5177