SOLUTION
This is a binomial probability. For i, we will apply the Binomial probability formula
i. Exactly 2 are defective
Using the formula, we have

Note that I made the probability of being defective as the probability of success = p
and probability of none defective as probability of failure = q
Exactly 2 are defective becomes the binomial probability
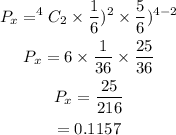
Hence the answer is 0.1157
(ii) None is defective becomes
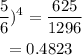
hence the answer is 0.4823
(iii) All are defective
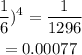
(iv) At least one is defective
This is 1 - probability that none is defective
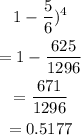
Hence the answer is 0.5177