Question

Jill and Bill are the same age. Jill inherits $20,000 when she is 25, and invests it in an account earning 5% annual interest rate, compounded annually. Bill receives a $20,000 bonus at age 35, and then invests it in an account which also earns a 5% annual interest rate, compounded annually. How much more money does Jill have than Bill at age 50?

A) $0
B) $10,000
C) $18,075
D) $26,149

Answer 1

D) 26,149 is the correct answer

Answer 2

Option D $26149 is correct.

Explanation:

It is given, at the age of 25, Jill had $20,000 and he invested it in an account earning at a rate of 5% compounded annually.

We have to find how much Jill will earn at a age of 50.

We will use compound interest formula. The formula is,

A = P ( 1+r)
`^(t)`

Where, A = last amount, P = principal amount, r = rate of interest, t = number of years.

P = 20000, r = 5% =
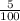`(5)/(100)` = 0.05,

t = (50-25) = 25

By substituting the values in the formula we will get,

A = 20000 (1 + 0.05)
`^(25)`

A = 20000 (1.05)
`^(25)`

A = 20000 (3.38635494)

A = 67727.10 ( Approximately taken upto two decimal place)

So we have got Jill will get at the age of 50 is $ 67727.10.

Now given, Bill had $20000 at the age of 35. He also invested it in an account which earns at a rate of 5% compounded annually.

Similarly we have to find the amount he will get at the age of 50.

So, P = $20000, r = 0.05, t = (50 - 35) = 15 years.

A = 20000 (1 + 0.05)
`^(15)`

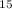
A = 20000 ( 1.05)
`^(15)`

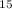
A = 20000 (2.078928)

A = 41578.56

So we have got at the age of 50 Bill will get $ 41578.56.

At the age of 50, Jill have more money than Bill. The amount of money that Jill have more = $(67727.10 - 41578.56) = $26148.54 rounded to $26149.

So we have got the answer.

Option D is correct here.