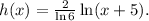1. The equation is
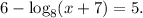
Rearranging, we have
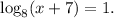
We know that (x+7) must be 8, since
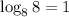
, so we set the equation:
x+7=8, which means that x=1.
(quick check:
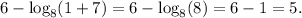
2.
The equation is
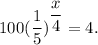
Dividing both sides by 100, the right hand side becomes 1/25, which can be written as

.
Now that both exponential expressions have the same base, we set the exponents equal:
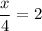
, which gives us x=8.
3.
The most well known natural logarithmic function is
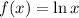
(that is:
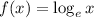
.)
The asymptote of this function is the line x=0. This means that we have to shift
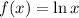
5 units left, to get:
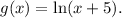
Now, at 1, this function takes the value

To make the function pass through (1, 2), we could multiply by
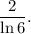
So, the function would be
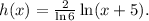
Answers:
1. 1
2. 8
3.