Question

What value is a discontinuity of quantity x squared plus 3 x minus 4 divided by quantity x squared plus x minus 12

Answer 1

(x² + 3x + 4) / (x² + x - 12)

Note that you can't divide by zero, and discontinuities are a result of that. We are looking for:
x² + x - 12 = 0
(x + 4)(x - 3) = 0
x = 3, -4

a. is one of those values, and is the answer.

Answer 2

x=3 is the point of discontinuity.

Explanation:

We have been given the expression:

`(x^2+3x-4)/(x^2+x-12)`

We have to find the discontinuity

To find the discontinuity we first have to factorize the given expression

`(x^2+4x-x-4)/(x^2+4x-3x-12)`

`\Rightarrow(x(x+4)-1(x+4))/(x(x+4)-3(x+4))`

`\Rightarrow((x-1)(x+4))/((x-3)(x+4))`

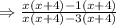
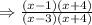
Cancel out the common factors from the numerator and denominator which is (x+4) so, we get:

`\Rightarrow((x-1))/((x-3))`

x=-4 is zero for both numerator and denominator.

Hence, put x=-4 in the above equation we get

`\Rightarrow((4-1))/((4-3))=3`

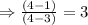
Hence, x=3 is the point of discontinuity.