Answer:
Option (b) is correct.
The length of ladder is 30 ft.
Explanation:
Given : A ladder is leaning against the side of a building and the base of the ladder is 12 ft from the building.
We have to find the length of ladder.
Consider the given data,
BC be the height of building and AB be the ladder.
and AC to the base of the ladder is 12 ft from the building.
measure of angle A = 70°
We have to determine BC.
Using trigonometric ratio,
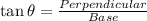
Here, for
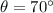 we have,
we have,
Perpendicular = BC and base = 12 ft
Substitute, we have,
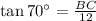
Solve, for BC, we have.
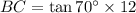
BC = 32.96 ft
So from the given options nearest feet is 30 ft.
Thus, The length of ladder is 30 ft.