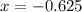Answer:
Vertex:
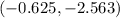
Axis of symmetry:
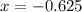
Explanation:
The function is given by the equation:
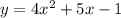
In general for any quadratic equation of the type:
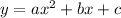
The coordinate of the vertex is: (h,k)
where
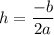
and
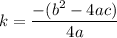
and the equation of axis of symmetry is:
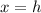
Here we have:
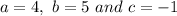
i.e.
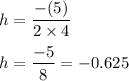
and
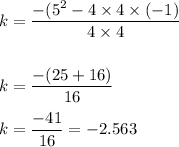
Hence, the vertex is:
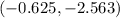
and the axis of symmetry is given by: