Question

David determines that 3 square root 2 cis(7pi/4) = -3+3i. When he considers the graphical representation of thesenumbers, he knows he made an error. Clearly explain in complete sentences what David observed, andwhere David made his mistake. State the correct rectangular equivalence of 3 square root 2 cis(7pi/4)

Answer 1

Step-by-step explanation

From the statement, we have the following complex number:

`z=3√(2)\cdot e^(i7\pi/4).`

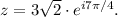
We must check graphically that this number is not equal to z' = -3 + i.

(1) The complex number z has:

• magnitude r = 3√2,

,

• angle θ = 7π/4 = 315°.

Plotting this complex number, we get the graph:

(2) The complex number z' = -3 + 3i has cartesian coordinates:

• x' = -3,

,

• y' = 3.

Plotting this complex number, we get:

We see that the complex number z' has:

• magnitude:

`z=\sqrt{x^(\prime2)+y^(\prime2)}=√((-3)^2+3^2)=2√(3),`

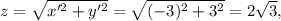
• angle:

`\theta^(\prime)=\tan^(-1)((y^(\prime))/(x^(\prime)))=\tan^(-1)((-3)/(3))=(\pi)/(4).`

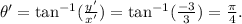
(3) Comparing the results from above, David observes that the two complex numbers:

• are not equal, z ≠ z',

,

• have the same magnitude r = 2√2,

,

• have different polar angles.

So David's mistake is in the angle of each complex number. Which represents a change in the signs of the rectangular components of z.

The correct rectangular equivalence of z is:

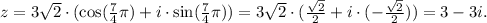
`z=3√(2)\cdot(\cos((7)/(4)\pi)+i\cdot\sin((7)/(4)\pi))=3√(2)\cdot((√(2))/(2)+i\cdot(-(√(2))/(2)))=3-3i.`Answer

• David's mistake is in the angle of each complex number. Which represents a change in the signs of the rectangular components of z.

• The correct rectangular equivalence of z is:

`z=3-3i`