Here you need to calculate the magnitude and phase angle of the quantity 2 + 2i.
The magnitude is found using the Pyth. Thm. and is sqrt(2^2 + 2^2), or
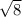
, or 2
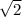
Recognize that the phase angle is 45 deg, or
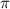
/4 rad.
Thus, the complex form is (2sqrt(2) angle
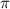
/4 rad ).