Question

a student wants to save $8,000 for college in 5 years how much should be put into an account that pays 5.2% annual interest compounded continuously

Answer 1

you use this formula

amount=principal(1+r%)^n
where
amount= the needed money to have been saved after five years for the student to join college=$8000
principal=the amount needed to be saved/invested in the account to give amount $8000 at the end of fifth year.
r=the rate of interest
therefore
$8000=p(1+5.2/100)^5
$8000=p(1+0.052)^5
$8000=p(1.052)^5
$8000=p(1.288483018284032)
$8000/(1.288483018284042)=p
$6208.851716691=p
p=$6208.8517

Answer 2

You will want to use the formula for continuously compounded interest:


`A = Pe^(rt)`

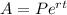
where
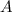
`A` is the resulting amount,
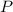
`P` is the initial amount,
`e` is the mathematical constant (2.718...),
`r` is the interest (in percentage), and
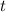
`t` is the time in years. Plugging these numbers into the equation gives the following:


`8000 = Pe^(0.052 * 5)`

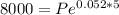
Solving for
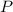
`P` will give you the initial amount that should be put into the account.