Answer : The area of triangle B is 4 times greater than the area of triangle A.
Step-by-step explanation :
Let the base of a triangle B be, x and the height of a triangle B be, y.
As we are given that, the base and the height of triangle A are half the base and the height of triangle B.
So, the base triangle A =
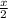
and, the height triangle A =

Now we have to determine the area of triangle A and B.
Formula used :

Area of triangle A =
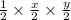
Area of triangle A =
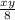
and,
Area of triangle B =
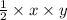
Area of triangle B =
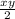
Now we have to take ratio of triangle A and B.

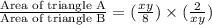
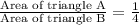
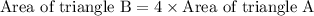
Hence, the area of triangle B is 4 times greater than the area of triangle A.