Question

Write an equation for the translation of
`y=(4)/(x)` that has the asymptotes x = 7 and y = 6.

Show all your steps, then graph it. (Be sure to link your graph with your steps.)

a.)
`y=(4)/(x+7)+6`
b.)
`y=(4)/(x-6)+7`
c.)
`y=(4)/(x+6)+7`
d.)
`y=(4)/(x-7)+6`

Answer 1

`\boxed{\boxed{\sf~y=(4)/(x-7)+6}}`

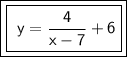
Solution Steps:

______________________________

1.) Substitute x, y, and general form using the formulas:

• Formula for x:
  `x=d=7`

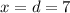
• Formula for y:
  `y=k=6`

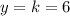
• Formula for general form y:
  `y=(a)/(x-d)+k=y=(4)/(x-7)+6`

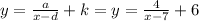
Note:

- When doing problems like this, it's best to list out each formula and do the drag down method, and replace methods rather than doing it the entire mathematical way, as doing it that way takes a long time and it's more confusing than it should be.

Equation at the end of Step 1:

• 
  `y=(4)/(x-7)+6`

2.) Simplify the d and k forms:

• 
  `y=(4)/(x-7)+6=y=(4)/(x-7)+6`

Note:

- The x(d) stays the same since the 7 was positive and we plugged it in making it negative, so it doesn't need to be changed. (Another way to know if you need to change it is if the original
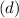`(d)` or
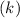`(k)` when plugged in, you had to put them in parenthesis then most likely it needs to be changed.

- The y(k) stays the same since the 6 was positive and we plugged it, keeping it positive so it doesn't need to be changed. (Another way to know if you need to change it is if the original
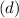`(d)` or
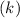`(k)` when plugged in, you had to put them in parenthesis then most likely it needs to be changed.

So the answer is d,
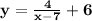`\bold{y=(4)/(x-7)+6}`.

______________________________