Question

Rationalize and simplify completely: √6 over √5

Answer 1

For this to be simplified completely, there cannot be a square root in the denominator of the fraction. So to simplify this, you must multiply the top and bottom of the fraction by √5


`( √(6) )/( √(5) ) * ( √(5) )/( √(5) )`

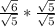
When you multiply a square root by itself you get the number that is under the square root. This means hat when we multiply √5 by √5 it becomes 5.

For the top of the fraction when we multiply √6 by √5 we multiply the 6 and 5 together and keep it under the square root.

Thus making
`( √(6) )/( √(5) ) * ( √(5) )/( √(5) )` ...


`( √(30) )/(5)`

Hope this helps!

Answer 2

The only thing to this is...


`\mathrm{Combine\:same\:powers}\:: (√(x))/(√(y))=\sqrt{(x)/(y)} \ \textgreater \ \sqrt{(6)/(5)}`

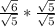
Hope this helps!