Question

Divide 3x^3+3x^2+2x-2 by x+3 using long division

Answer 1

3x^3+3x^2+2x-2 | x+3
--------------------
-3x^3 -9x^2 3x^2 - 6x+20
------------------------
/ -6x^2+2x+2
+6x^2 +18x
-----------------------
/ 20x+2
-20x -60
-----------------
/ -58

(3x^3+3x^2+2x-2 ) : (x+3)= 3x^2 - 6x+20 and the rest is -58

Answer 2

Quotient = 3x² - 6x + 20

Remainder = -62

Explanation:

In long division, we follow the following steps.

Step 1 : write the dividend under the division symbol, and the divisor to the left on the outside.

Step 2 : Divide the first expression.

Step 3 : write the remainder obtained from the first division and write the third expression it will be the new dividend

Step 4 : again divide the dividend write the remainder and fourth expression as a new dividend.

Step 5 : Repeat these steps until you get the expression which is of less degree than the divisor.

Here, the given expression,

`(3x^3+3x^2+2x-2)/(x+3)`

Using above steps,

We obtained,

`(3x^3+3x^2+2x-2)/(x+3)=3x^2-6x+20-(62)/(x+3)`

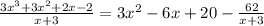
i.e. Quotient = 3x² - 6x + 20

Remainder = -62