Question

PLEASE HELP!!!!! The data set below shows the number of homework assignments required in math classes for a month:

22

23

23

21

18

4

17

15

23

20

24

15

25

16



Which of the following statements is true based on the data set?
There is one outlier that indicates an unusually large number of assignments required in that class.
There is one outlier that indicates an unusually small number of assignments required in that class.
There are two outliers that indicate an unusually large number of assignments required in those two classes.
There are two outliers that indicate an unusually small number of assignments required in those two classes.

Answer 1

There is one outlier that indicates an unusually small number of assignments required in that class.

Explanation:

I took the test and got it correct.

Answer 2

The correct option is 2.

Explanation:

The given data set is

22, 23, 23, 21, 18, 4, 17, 15, 23, 20, 24, 15, 25, 16

Arrange the data is ascending order.

4, 15, 15, 16, 17, 18, 20, 21, 22, 23, 23, 23, 24, 25

Divide the data in 4 equal parts.

(4, 15, 15), 16, (17, 18, 20), (21, 22, 23), 23, (23, 24, 25)

Now, we can say that

`Q_1=16`

`Q_3=23`

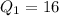
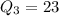
The interquartile range of the data set is

`IQR=Q_3-Q_1=23-16=7`

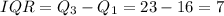
If the data lie in the interval
`[Q_1-1.5(IQR),Q_3+1.5(IQR)]`, then the data set has not outliers.

`[Q_1-1.5(IQR),Q_3+1.5(IQR)]=[16-1.5(7),23+1.5(7)]\Rightarrow [5.5,33.5]`

All the data lie in the interval [5.5,33.5] except 4. So, 4 is an outlier of the given data.

There is one outlier that indicates an unusually small number of assignments required in that class. Therefore the correct option is 2.