Question

Which equation represents the hyperbola that has its Foci farthest from its Center

Answer 1

b

Explanation:

Answer 2

Equation of hyperbola is given by

`((x-h)^2)/(a^2)- ((y-k)^2)/(b^2)=1`

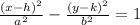
Where the centre is (h, k) and the foci is (h-c, k) and (h+c, k)

c is obtained from
`c^2=a^2+b^2`

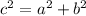
We'll calculate the distance for each option in turn

Option A


`((x-2)^2)/(8^2)- ((y-1)^2)/(7^2)=1`

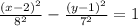
The centre is (2, 1)

Work out the value of 'c' to find the coordinates of two focus
We have
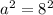
`a^2=8^2` and
`b^2=7^2`

`c^2=a^2+b^2=8^2+7^2=64+49=113`

`c= √(113)`

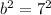
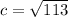
The coordinate of foci is
`(2- √(113), 1)` and
`(2+ √(113), 1)`

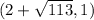
Notice that the y-coordinate of the focus is the same with the y-coordinate of the centre, so we'll only need to work out the horizontal distance between one foci to the centre (the centre of a hyperbola is the same distance to both focus)

Distance from foci to centre =
`(2+ √(113))-2=12.6-2=10.6`
--------------------------------------------------------------------------------------------------------------

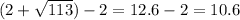
Option B

Centre (-2, 3)
c² = a² + b² = 19² + 11² = 482
c = √482
c = 21.95

The coordinates of focus = (-2+21.95, 3) and (-2-21.95, 3)
= (19.95, 3) and (-23.95, 3)

Distance from one foci to the centre is = 19.95 - (-2) = 21.95 units
If the other foci is used for the calculation, the answer will be the same
---------------------------------------------------------------------------------------------------------------

Option C

Centre (1, 2)
c² = 6² + 9² = 36 + 81 = 117
c = √117
c = 10.8

Coordinates of focus = ((1-10.8), 2) and ((1+10.8), 2)
= (-9.8, 2) and (11.8, 2)

Distance between foci and centre = 11.8 - 1 = 10.8 units
----------------------------------------------------------------------------------------------------------

Option D

Centre (5, -3)

c² = 5² + 19² = 386
c = √386
c = 19.6

Coordinates of focus are ((5-19.6), -3) and ((5+19.6), -3) = (-14.6, -3) and (24.6, -3)

Distance foci - centre = 24.6 - 5 = 19.6
--------------------------------------------------------------------------------------------------------------

The equation that gives the furthest distance from centre to foci is given by option B