Question

In a randomly generated sequence of 24 binary digits (0s and 1s), what is the probability that exactly half of the digits are 0? a. 1352078 b. 1.295 c. 0 d. 0.1612 Please select the best answer from the choices provided A B C D

Answer 1

0.1612

Explanation:

We are given that there are 24 binary digits .

We are supposed to to find the probability that exactly half of the digits are 0.

Probability of success p (getting half of 24 i.e. 12 digits is 0 ) = 0.5

Since the sum of the probabilities is 1 .

So, probability of failure q = 1-0.5 = 0.5

Formula :
`P(x)=^nC_r {\cdot} (p)^r {\cdot} (q)^(n-r)`

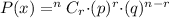
So, n = 24

r = 12

p = 0.5

q=0.5

Substituting the values we get :

`P(x)=^(24)C_12 {\cdot} (0.5)^(12) {\cdot} (0.5)^(24-12)`

`P(x)=(24!)/(12!* (24-12)!)(0.5)^(12) {\cdot} (0.5)^(12)`

`P(x)=2704156* 0.000244140625* 0.000244140625`

`P(x)=0.16118`

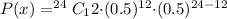
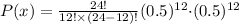
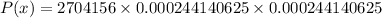
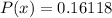
Thus the probability of exactly half of the digits are 0 is 0.1612

Hence Option D is correct .

Answer 2

P(X=12) = 24C12 * (0.5)^12 * (0.5)^12
= 0.161 to 3 d.p.

not entirely sure, but i think it's that