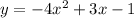Question

Use a system of equations to find the parabola of the form yequals=axsquared2plus+bxplus+c that goes through the three given points. ​(22​, negative 11−11​), ​(negative 2−2​, negative 23−23​), ​(44​, negative 53−53​)

Answer 1

Given that a parabola of the form
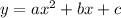
`y=ax^2+bx+c` passing through the points (2, -11), (-2, -23) and (4, -53)

Thus, substituting the points we have:


`-11=(2)^2a+2b+c \\ \\ \Rightarrow-11=4a+2b+c\ .\ .\ .\ (1) \\ \\ -23=(-2)^2a+(-2)b+c \\ \\ \Rightarrow -23=4a-2b+c\ .\ .\ .\ (2) \\ \\ -53=(4)^2a+4b+c \\ \\ \Rightarrow-53=16a+4b+c\ .\ .\ .\ (3)`

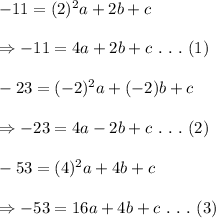
We solve equations (1), (2) and (3) simulataneously. (There are many mays it can be solved but I will use row reduction method here).

We form the augumented matrix for equations (1), (2) and (3) and perform elementary row operations as follows:


`\left[\begin{array}{ccc}4&2&1\\4&-2&1\\16&4&1\end{array}\right| \left.\begin{array}{c}-11\\-23\\-53\end{array}\right] \ \ \ \ \ (1)/(4) R_1\rightarrow R_1 \\ \\ \left[\begin{array}{ccc}1& (1)/(2) & (1)/(4) \\4&-2&1\\16&4&1\end{array}\right| \left.\begin{array}{c}- (11)/(4) \\-23\\-53\end{array}\right] \ \ \ \ \ {{-4R_1+R_2\rightarrow R_2} \atop {-16R_1+R_3\rightarrow R_3}}`


`\left[\begin{array}{ccc}1& (1)/(2) & (1)/(4) \\0&-4&0\\0&-4&-3\end{array}\right| \left.\begin{array}{c}- (11)/(4) \\-12\\-9\end{array}\right] \ \ \ \ \ - (1)/(4) R_2 \\ \\ \left[\begin{array}{ccc}1& (1)/(2) & (1)/(4) \\0&1&0\\0&-4&-3\end{array}\right| \left.\begin{array}{c}- (11)/(4) \\3\\-9\end{array}\right] \ \ \ \ \ {{ -(1)/(2) R_2+R_1\rightarrow R_1} \atop {4R_2+R_3\rightarrow R_3}}`


`\left[\begin{array}{ccc}1&0& (1)/(4) \\0&1&0\\0&0&-3\end{array}\right| \left.\begin{array}{c}- (17)/(4) \\3\\3\end{array}\right] \ \ \ \ \ - (1)/(3) R_3 \\ \\ \left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right| \left.\begin{array}{c}-4\\3\\-1\end{array}\right] \ \ \ \ \ - (1)/(4) R_3+R_1\rightarrow R_1`

Thus, a = -4, b = 3, c = -1

Therefore, the required polynomial is
`y=-4x^2+3x-1`