Question

The time (in number of days) until maturity of a certain variety of hot pepper is normally distributed, with mean μ and standard deviation σ = 2.4. this variety is advertised as taking 70 days to mature. i wish to test the hypotheses h0: μ = 70, ha: μ > 70, so i select a simple random sample of four plants of this variety and measure the time until maturity. the four times, in days, are 76 73 69 70 based on these data, i would reject h0 at level:

Answer 1

From the sample,


`\bar{x}= (76+73+69+70)/(4) \\ \\ = (288)/(4) =72`

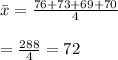
The test statistics is given by:


`z= \frac{\bar{x}-\mu}{\sigma/√(n)} = (72-70)/(2.4/√(4)) = (2)/(1.2) =1.67`

The null hypothesis is rejectted when the z-value of the test statistics is greater than the z-value of alpha/2

i.e. the rejection region is


`1.67\geq z_(\alpha/2) \\ \\ \Rightarrow z_(1-0.9525)\geq z_(\alpha/2) \\ \\ \Rightarrow\alpha/2=0.0475 \\ \\ \Rightarrow\alpha=0.095`

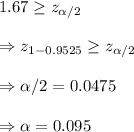
Therefore, based on the given data, the null hypothesis will be rejected at a significant level of 0.095.