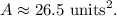Recall that the sine law states that:
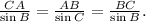
Therefore:
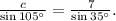
Solving for c we get:
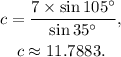
Now, we know that the interior angles of a triangle add up to 180 degrees, therefore the measure of angle A is:
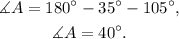
Using the sine law we get:
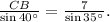
Solving the above equation for CB we get:
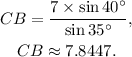
Finally, using Heron's formula we get that the area of the given triangle is:
![\begin{gathered} A=\sqrt[]{13.3165(13.3165-7.8447)(13.3165-11.7883)(13.3165-7)}, \\ A=\sqrt[]{13.3165(5.4718)(1.5282)(6.3165)}, \\ A\approx\sqrt[]{703.3589}, \\ A\approx26.5. \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/8evl7qkojca92rew4be5.png)
Answer: