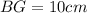Question

Will owe you. "DG¯¯¯¯¯¯ , EG¯¯¯¯¯ , and FG¯¯¯¯¯ are perpendicular bisectors of the sides of △ABC . CF=8 cm and FG=6 cm.

What is BG ?

Enter your answer in the box."

Answer 1

the correct answer is 10

Answer 2

`BG = 10cm`

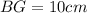
Explanation:

The intersection of all three perpendicular bisector is called the circumcenter, which is an equidistant point from each vertex of the triangle, that is

`AG \cong CG \cong BG`

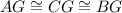
So, to find the answer, we just have to find the length of CG, and that would be also the length of BG.

Now, let's focus in the
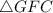`\triangle GFC`, which is a right triangle and CG is the hypothenuse, applying pythagorean's theorem, we have

`CG^(2)=CF^(2)+FG^(2)`

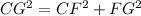
But, we know that
`CF=8;FG=6`

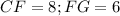
Replacing this values, we have

`CG^(2)=8^(2)+6^(2)\\CG=√(64+36)=√(100)\\ CG=10`

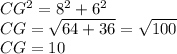
Remember that
`CG = BG`

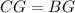
Therefore,
`BG = 10cm`