Question

This is for a Harmonic Motion function. (If we get through this entire section: I will write a very long letter of gratitude and give you the highest rating for helping me understand. I truly just want to finish) There are only 10 short questions left... I know we can do this. Here is what I got so far :•Period of pendulum:1.6•B value (rounded to the nearest thousandth): 3.762 rad/s•Amplitude, in meters(rounded to the nearest thousandth):0.733m•Trigonometric function that starts at its peak of amplitude: Sine•Harmonic motion formula for the base scenario: f(Ø)=0.733sin(3.762(60-c))+dNOW, it is time to analyze it. Using the information that I have and the function given, I need to write a statement that represents all of the times where the pendulum is at its resting position. (These are the points in time where the pendulum has a position of zero) what is the statement for the zeros of the base harmonic motion function? Explain(the base function is used to find the position of the pendulum at any given point in time. )describe where the pendulum is located at 10 seconds , include the distance from the resting position , rounded to the nearest thousandth. Next, we change the starting angleJust repeat the same process, but with a different starting angle. Start the pendulum at 30 (change the 60 for 30)how will the new starting angle of 30 affect the pendulum and its harmonic motion function? Explain. (find the harmonic function that represents the pendulum that has a starting angle at 30)What is the harmonic motion function that represents the position of the pendulum when it is started from 30? How does starting the pendulum at 30 compare to the base scenario at 60? Explain.Time to change the length of the pendulum (the starting angle will be 60, but the length of the pendulum will be shortened to 0.4 meters.)How do you think shortening the pendulum to 0.4 m will affect the pendulum and it's equation? Explainwhat is the harmonic motion function for the pendulum when the length of the pendulum is shortened to 0.4 meters? explain how changing the length of the pendulum affected the function the way that it did. SET OF QUESTIONS: (start with your base harmonic motion function from the first time. Keeping the same a value, replace the b value with 4.5)explain how replacing the b value in the base harmonic motion function from stage first time , will affect it. What is the amplitude of the new harmonic motion function. Explain. what is the period of the new harmonic motion function? Explain. Using the new harmonic motion function, how many periods will the pendulum complete over the course of 60 seconds? Explain. (If you made it this far, I would like to thank you for your service and patience with my tedious questions. Thank you for granting me the ability to see the understanding of these questions. You are greatly appreciated)

Answer 1

Function of basic harmonic motion is as follows:

`x(t)=A\sin (\omega t+\phi)`

Here,

`A\text{ is amplitude, }\omega\text{ is angular frequency of harmonic motion, }\phi\text{ is initial phase}`

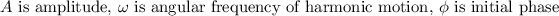
If pendulum starts from position zero, at position zero phase of pendulum is zero.

Hence, function of harmonic motion is as follows:

`x(t)=A\sin (\omega t)`

Function given for this case is,

`x(t)=0.733\text{ sin (3.762t) }\ldots(1)`

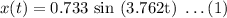
Statements for zeros:

When net force acting on pendulum is zero, pendulum is in its equilibrium condition.

Which means that, at equilibrium position restoring force due to gravity and tession in a cord of pendulum becomes identical.

Now, at time (t = 0), position of pendulum is at (x=0),

Here, x=0 is equilibrium position of pendulum.

Position of pendulum at 10 seconds is as follows:

Substitute values of time in equation-(1),

`\begin{gathered} x(10)=0.733\sin (3.762*10) \\ x(10)=0.733\text{ (-0.079)} \\ x(10)=-0.058\text{ m} \end{gathered}`

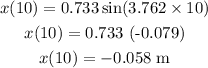
If starting angle of pendulum is,

`\begin{gathered} \phi=60^o \\ \phi=(\Pi)/(3) \end{gathered}`

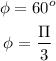
Step-2:

Hence, Initial function of pendulum is,

`x(t)=0.733\sin (3.762t+(\Pi)/(3))\ldots(2a)`

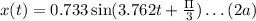
Now, changing the starting angle,

`\text{from 60}^oto30^o`

Function that repersents the position,

`x(t)=0.733\text{ sin (3.726t+}(\Pi)/(6)\text{) }\ldots.(2)`

Step-3:

Now, starting angle of pendulum is,

`\phi=60^o`

Length of pendulum is,

`l=0.4\text{ m}`

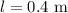
Period of pendumum is,

`T=2\Pi\sqrt[]{(l)/(g)}`

Substitute known values in above equation,

`\begin{gathered} T=2*3.14\sqrt[]{(0.4)/(9.8)} \\ T=1.27\text{ seconds} \end{gathered}`

Angular frequency of pendulum is as follows:

`\begin{gathered} \omega=(2\Pi)/(T) \\ \omega=\frac{2\Pi}{1.27\text{ s}} \\ \omega=4.944\text{ rad/s} \end{gathered}`

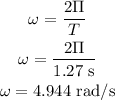
Now, new function of pendulum is,

`x(t)=0.733\text{ sin (4.944t+}(\Pi)/(3)\text{)}`

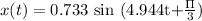
Step-4:

Now, replacing value of angular frequency,

`\omega=4.5\text{ }`

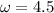
Amplitude of pendulum will not change. Because, amplitude of pendulum does not depends on angular frequency of pendulum.

Period of new harmonic function is as follows:

Formula of period in terms of angular frequency is as follows:

`\begin{gathered} T=(2\Pi)/(\omega) \\ T=\frac{2*3.14}{4.5\text{ rad/s}} \\ T=1.4\text{ seconds} \end{gathered}`

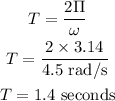
Formula of number of period compeleted by pendulum is as follows:

`n=(t)/(T)`

Number of period compeletd by pendulum in t = 60 seconds,

Substitute known values in above equation,

`\begin{gathered} n=\frac{60\text{ s}}{1.4\text{ s}} \\ n=42.85 \end{gathered}`

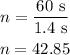
42 periods compeleted by pendulum in 60 seconds.