Given:
Count in bacteria culture after 20 minutes = 200
Count in bacteria culture after 40 minutes = 1900
Required: Find the initial size, doubling period, population after 60 minutes and time at which the population will reach 11000
Explanation:
The exponential growth can be modeled by
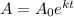
where A0 is the initial size and k is the growth rate.
Plug the condition A(20) = 200.
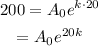
Plug the condition A(40) = 1900.
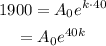
Divide both of them.
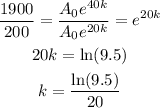
Thus,

Substitute A(20) = 200 to find the initial count.
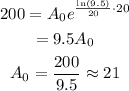
Thus,
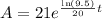
To find the doubling, find t at which A(t) = 42.
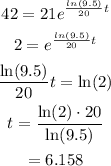
The doubling time is 6.158 minutes.
To find the population after 60 minutes, substitute 60 for t into A(t).
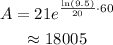
The count of bacteria after 60 minutes is 18005.
To find the time required for the culture of 11000, find t at which A(t) = 11000.
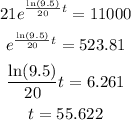
The count of bacteria will reach 11000 in 55.622 minutes.
Final Answer:
Initial count = 21
The doubling time is 6.158 minutes.
The count of bacteria after 60 minutes is 18005.
The count of bacteria will reach 11000 in 55.622 minutes.