Tow rates are equivalent if tow initial investments over a the same time, produce the same final value using different interest rates.
For the annually rate we have that:

Where
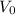
= initial investment.

= annually interest rate in decimal form.
And the exponent (1) represents the full year.
For the quarterly interest rate we have that:
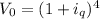
Where
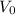
= initial investment.
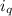
= quarterly interest rate in decimal form.
And the exponent (4) the 4 quarters in the full year.
Since the rates are equivalent if tow initial investments over a the same time, produce the same final value, then

Notice that we are not using the initial investment
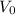
since they are the same.
The first thin we are going to to calculate the equivalent quarterly rate of the 7% annually rate is converting 7% to decimal form
7%/100 = 0.07
Now, we can replace the value in our equation to get:
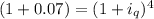
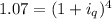
![\sqrt[4]{1.07} =1+ i_(q)](https://img.qammunity.org/2018/formulas/mathematics/high-school/5037w7akim96e95r6dovuxw6yrlxalzk85.png)
![i_(q) = \sqrt[4]{1.07} -1](https://img.qammunity.org/2018/formulas/mathematics/high-school/8pmxt2e8hlmp8bg103ubf05bu36q7hwqva.png)
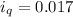
Finally, we multiply the quarterly interest rate in decimal form by 100% to get:
(0.017)(100%) = 1.7%
We can conclude that Alexander is wrong, the equivalent quarterly rate of an annually rate of 7% is 1.7% and not 2%.