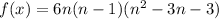Let
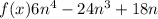
First thing I notice is that all those terms are multiples of 6 and n so we can pull those straight out,
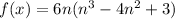
Now the trickier part, notice if we let n=1 then

. By the factor-remainder theorem this means

is a factor of
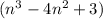
.
Now perform polynomial division, dividing

into
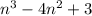
. You are left with the quotient
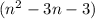
hence