Question

Write an equation for the translation of
`y=(-7)/(x)` that has the asymptotes x = -4 and y = -8.

Show your all your steps, then graph it. (Be sure to link your graph to your steps.)

a.)
`y=(-7)/(x-8)-4`
b.)
`y=(-7)/(x+4)-8`
c.)
`y=(-7)/(x+8)-4`
d.)
`y=(-7)/(x-4)-8`

Answer 1

`\boxed{\boxed{\sf~y=(-7)/(x+4)-8}}`

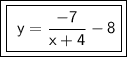
Solution Steps:

______________________________

1.) Substitute x, y, and general form using the formulas:

• Formula for x:
  `x=d=-4`

• Formula for y:
  `y=k=-8`

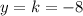
• Formula for general form y:
  `y=(a)/(x-d)+k=y(-7)/(x-(-4))+(-8)`

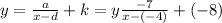
Note:

- When doing problems like this, it's best to list out each formula and do the drag down method, and replace methods rather than doing it the entire mathematical way, as doing it that way takes a long time and it's more confusing than it should be.

Equation at the end of Step 1:

• 
  `y=(-7)/(x-(-4))+(-8)`

2.) Simplify the d and k forms:

• 
  `y=(-7)/(x-(-4))+(-8)=y=(-7)/(x+4)-8`

Note:

- The x(d) changes from
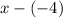`x-(-4)` to
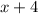`x+4` because of the 2 negatives rule: When there is 2 negatives next to each other, it automatically changes to being the positive version of of that number or the sum of the 2 numbers.

- The y(k) changes from
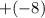`+(-8)` to
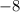`-8` because when a
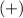`(+)` and
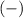`(-)` are next to each other, the rule is
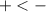`+<-`. The Minus always wins in this type of problem situation.

So the answer is b,
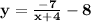`\bold{y=(-7)/(x+4)-8}`.

______________________________