Question

The population of a type of local frog can be found using an infinite geometric series where a1 = 84 and the common ratio is one fifth. Find the sum of this infinite series that will be the upper limit of this population.

Answer 1

The series is 84(1+1/5+1/25+...)=84(1/(1-1/5)=84÷4/5=84×5/4=21×5=105. Upper limit is 105.

Answer 2

The sum is 105

Explanation:

Given that the population of a type of local frog can be found using an infinite geometric series where a1 = 84 and the common ratio is one fifth.

we have to find the sum

`\text{Common ratio}=r=(1)/(5)<1`

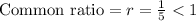
If
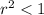`r^2<1` infinite series converges, otherwise it diverges.

Since the sum of any geometric sequence is:

`S_n=(a(1-r^n))/((1-r))`

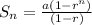
whenever
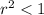`r^2<1` the sum of the infinite series is

`S_n=(a)/((1-r))`

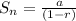
Since a=84 and
`r=(1)/(5)` the sum of infinite series

`S_n=(84)/((1-(1)/(5)))`

`=(84)/((4)/(5))`

`=(5*84)/(4)=105`

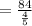
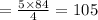
Hence, the sum is 105