Answer:
A. Parallel
Explanation:
Given: Equations
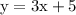 and
and
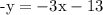
To Find: whether the graphs of y = 3x + 5 and -y = -3x - 13 are parallel, perpendicular, coincident, or none of these.
Solution:
As Equations are linear
Equation of Line 1 =
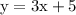
Equation of Line 2 =
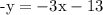
We know that,
standard equation of line is,
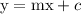
writing equation of lines in standard form
Line 1,
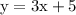
Line 2,
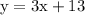
Comparing with standard equations we find out that
Slope of Line 1=

Slope of Line 2=

therefore graphs of both equations is parallel, now we have to check if they are coincidental
intercept
 of line 1 =
of line 1 =
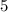
intercept
 of line 2 =
of line 2 =
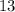
intercept
 of line 1 ≠ intercept
of line 1 ≠ intercept
 of line 2
of line 2
Graphs are not coincidental
Therefore Option A is correct Graphs of both equations are parallel.