Question

11.) In the given figure, IJKL is an isosceles trapezoid with base LK = 16 and 1) = 8.If I = R = 5, then what is the area of the trapezoid?A 24 cmB 36 cm1C 45 cmKD 89 cm?GO ON12.) What is the value of x?

Answer 1

Area of an trapezoidal is express as :

`Area\text{ = }\frac{Sum\text{ of Parallel sides}}{2}* Height\text{ of trapezoid}`

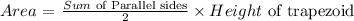
So, to find the height of trapezium we draw a perpendicular from J to the base line LK and a perpendicular from I to the base line LK such that the MN= IJ

So, We have two right triangle JNK and IML

Apply Pythogaras in any one of the right triangle and find the length of perpendicular

In triangle JNK

`\begin{gathered} \text{From Pythagoras ,} \\ \text{Hypotenuse }^2+Perpendicular^2_{}+Base^2 \\ JK^2=JN^2+NK^2 \\ \text{Substitute the valus and solve for JN,} \\ 5^2=JN^2+4^2 \\ JN^2=25-16 \\ JN^2=9 \\ JN=3 \\ \text{ So, The perpendicular of triangle JN is 3} \end{gathered}`

Since, the perpendicular JN is also the height of trapezium,

Substitute the values

Height JN =3

Parallel Sides IJ = 8 and LK = 16

So, the Area of Trapezium will be

`\begin{gathered} \text{Area of trapezium IJKL =}\frac{Sum\text{ of parallel Sides}}{2}* Height \\ \text{Area of trapezium IJKL =}\frac{IJ\text{ +LK}}{2}* JN \\ \text{Area of trapezium IJKL =}(8+16)/(2)*3 \\ \text{Area of trapezium IJKL =}(24)/(2)*3 \\ \text{Area of trapezium IJKL =12}*3 \\ \text{Area of trapezium IJKL =}36cm^2 \end{gathered}`

Answer : B) 36 cm²