Question

What is the equation, in slope-intercept form, of the line that is perpendicular to the line y – 4 = –2/3(x – 6) and passes through the point (−2, −2)?

Answer 1

y+2=3/2(x+2)
y+2=3/2x+3
y=3/2x+1

Answer 2

The equation of required line is
`y=(3)/(2)x+1`.

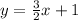Explanation:

If a line passes through a points
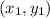`(x_1,y_1)` with slope m, then the point slope form of the line is

`y-y_1=m(x-x_1)`

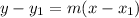
The given equation of line is

`y-4=-(2)/(3)(x-6)`

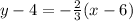
It means the slope of this line is
`-(2)/(3)`.

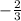Product of slopes of two perpendicular lines is -1. So, the slope of perpendicular line is
`(3)/(2)`.

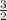The slope of required line is
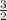`(3)/(2)` and it passes through the point (-2,-2). So, the equation of line is

`y-(-2)=(3)/(2)(x-(-2))`

`y+2=(3)/(2)(x+2)`

`y+2=(3)/(2)x+3`

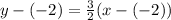
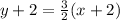
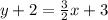
Subtract 2 from both sides.

`y=(3)/(2)x+3-2`

`y=(3)/(2)x+1`

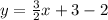
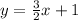
Therefore, the equation of required line is
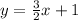`y=(3)/(2)x+1`.