Question

Find the indicated derivative.

Answer 1

`\displaystyle (d)/(dt) \bigg( ((9t - 8)^6)/(t + 2) \bigg) = ((9t - 8)^5(45t + 116))/((t + 2)^2)`

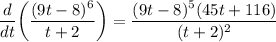
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Derivative Rule [Quotient Rule]:
`\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))`

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Explanation:

Step 1: Define

Identify

`\displaystyle (d)/(dt) \bigg( ((9t - 8)^6)/(t + 2) \bigg)`

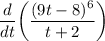
Step 2: Differentiate

1. Derivative Rule [Quotient Rule]:
   `\displaystyle (d)/(dt) \bigg( ((9t - 8)^6)/(t + 2) \bigg) = ([(9t - 8)^6]'(t + 2) - (9t - 8)^6(t + 2)')/((t + 2)^2)`
2. Basic Power Rule [Chain Rule, Multiplied Constant]:
   `\displaystyle (d)/(dt) \bigg( ((9t - 8)^6)/(t + 2) \bigg) = (6(9t - 8)^5(9t - 8)'(t + 2) - (9t - 8)^6)/((t + 2)^2)`
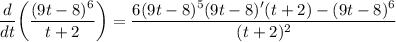
3. Basic Power Rule [Multiplied Constant, Addition/Subtraction]:
   `\displaystyle (d)/(dt) \bigg( ((9t - 8)^6)/(t + 2) \bigg) = (54(9t - 8)^5(t + 2) - (9t - 8)^6)/((t + 2)^2)`
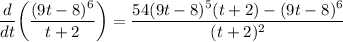
4. Factor:
   `\displaystyle (d)/(dt) \bigg( ((9t - 8)^6)/(t + 2) \bigg) = ((9t - 8)^5 \big[ 54(t + 2) - (9t - 8) \big] )/((t + 2)^2)`
5. Expand:
   `\displaystyle (d)/(dt) \bigg( ((9t - 8)^6)/(t + 2) \bigg) = ((9t - 8)^5 \big[ 54t + 108 - 9t + 8 \big] )/((t + 2)^2)`
6. Combine like terms:
   `\displaystyle (d)/(dt) \bigg( ((9t - 8)^6)/(t + 2) \bigg) = ((9t - 8)^5(45t + 116))/((t + 2)^2)`

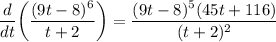
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation