Answer:
There are infinitely solutions to the system because the equations represent the same line.
Explanation:
The system of linear equations presented represents the same line. We can deduct that by multiplying the first one by -4:
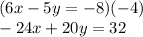
As you can observe, we get the same equation than the second one in the system, this means that they actually represent the same line. In other words, the solutions are all the common points, which are all of them possible, which are infinite.
Therefore, the right option is the last one.