Question

Need help with 7, 9, 11 plz ❤️

Answer 1

7)

f(x) = 2x² - 12x + 22

now, if you recall, in a perfect square trinomial, the middle term is a combination of the two other terms times 2, namely


`\bf \begin{array}{cccccllllll} {{ a}}^2& + &2{{ a}}{{ b}}&+&{{ b}}^2\\ \downarrow && &&\downarrow \\ {{ a}}&& &&{{ b}}\\ &\to &({{ a}} + {{ b}})^2&\leftarrow \end{array}\qquad % perfect square trinomial, negative middle term \begin{array}{cccccllllll} {{ a}}^2& - &2{{ a}}{{ b}}&+&{{ b}}^2\\ \downarrow && &&\downarrow \\ {{ a}}&& &&{{ b}}\\ &\to &({{ a}} - {{ b}})^2&\leftarrow \end{array}`

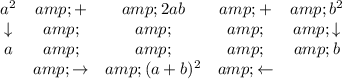
so let's us first do some grouping,

f(x) = (2x² - 12x) +22

f(x) = 2(x² - 6x) + 22

f(x) = 2(x² - 6x + [?]²) + 22

notice, we're missing a 3rd element in the group, to get a perfect square trinomial, hmmm what would that be?

well, let's see the middle guy, 6x, recall the middle guy is a combination of 2*a * b, therefore the middle term is 2 * x * b, and we know is 6x, thus


`\bf2x\boxed{?}=6x\implies \boxed{?}=\cfrac{6x}{2x}\implies \boxed{?}=3`

low and behold, our missing fellow is 3 then.

now, keep in mind that, if we add 3², we also have to subtract 3², since all we're doing is borrowing from our very good friend Mr Zero, 0, thus

f(x) = 2(x² - 6x +3² - 3²) + 22

f(x) = 2(x² - 6x +3²) + 22 -2*3² <---- notice the common factor 2 there.

f(x) = 2(x - 3)² + 22 - 18

f(x) = 2(x - 3)² +4

9)


`\bf ~~~~~~\textit{parabola vertex form} \\\\ \begin{array}{llll} y=a(x-{{ h}})^2+{{ k}}\\\\ x=a(y-{{ k}})^2+{{ h}} \end{array} \qquad\qquad vertex~~(\stackrel{}{{{ h}}},\stackrel{}{{{ k}}})\\\\ -------------------------------\\\\ h(x)=5(x+1)^2-45\implies h(x)=5[x-\stackrel{h}{(-1)}]^2\stackrel{k}{-45}`

11)

we know the roots are -2 and 3, therefore then, recall that a "solution" or a zero is really just referring to the x-intercepts, so -2 and 3 are really where the graph touches the x-axis, or the x-intercepts.

now, if x = -2, then x + 2 = 0 <--- this means (x+2) is a factor

if x = 3, then x - 3 = 0 <--- this means (x - 3) is a factor as well.

now if could have some other factors, like say 5, and that's fine, but we know that, since -2 and 3 are zeros, (x+2)(x-3) are part of it, so 5(x+2)(x-3) is very feasible.