Question

Gabriella is designing a flashlight that uses a parabolic reflecting mirror and a light source. The shape of the mirror can be modeled by (y+3)^2=26(x-2) where x and y are measured in inches. Where should she place the bulb to ensure a perfect beam of light?

Answer 1

the bulb should be placed at the "focus point" of the parabolic mirror.


`\bf \textit{parabola vertex form with focus point distance}\\\\ \begin{array}{llll} (y-{{ k}})^2=4{{ p}}(x-{{ h}}) \end{array} \qquad \begin{array}{llll} vertex\ ({{ h}},{{ k}})\\\\ {{ p}}=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix} \end{array}\\\\ -------------------------------\\\\`


`\bf (y+3)^2=26(x-2)\implies [y-\stackrel{k}{(-3)}]^2=\stackrel{4p}{26}(x-\stackrel{h}{2}) \\\\\\ 4p=26\implies p=\cfrac{26}{4}\implies p=\cfrac{13}{2}\\\\ -------------------------------\\\\ vertex~(2,-3)\qquad focus~\left(2+(13)/(2)~,~-3\right)`

check the picture below.

bear in mind that, because the leading term's coefficient is positive, namely for y², the parabola opens to the right, and "p" is positive, therefore the focus point will be to the right of the vertex.

Answer 2

Gabriella place the bulb at the focus of the parabola, i.e.,
`((17)/(2),-3)`.

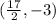Explanation:

It is given that the shape of the mirror can be modeled by

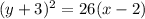`(y+3)^2=26(x-2)` ... (1)

where x and y are measured in inches.

The standard form of the parabola is,

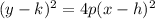`(y-k)^2=4p(x-h)^2` ... (2)

Where (h,k) is vertex and p is the difference between vertex and focus. The focus is (h+p,k)

On comparing (1) and (2) we get,

`k=-3,h=2,p=(13)/(2)`

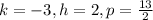
The vertex of the parabola is (3,-2) and the focus is

`(2+(13)/(2),-3)=((17)/(2),-3)`

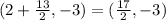
Gabriella place the bulb at the focus of the parabola, i.e.,
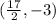`((17)/(2),-3)`.