Question

Evaluate 0.985 using the Binomial Theorem.

Write 0.98 as a binomial: (1 + _______)

Answer 1

Evaluate 098^5 using the binomial theorem

-0.02

Answer 2

The value of
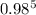`0.98^5` is 0.9039207968.

Explanation:

We need to find the value of
`0.98^5`.

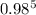According to the binomial theorem,

`(a+b)^n=^nC_0a^n+^nC_(1)a^(n-1)b+...+^nC_(n-1)a^1b^(n-1)+^nC_nb^n`

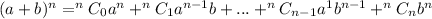
Write 0.98 as a binomial: (1 - 0.02)

Write 0.98 as a binomial: (1 + (-0.02))

`0.98^5=(1 + (-0.02))^5`

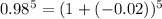
Using binomial theorem, we get

`0.98^5=^5C_0(1)^5+^5C_1(1)^4(-0.02)^1+^5C_2(1)^3(-0.02)^2+^5C_3(1)^2(-0.02)^3+^5C_4(1)^1(-0.02)^4+^5C_5(1)^0(-0.02)^5`

`0.98^5=(1)+5(-0.02)^1+10(-0.02)^2+10(-0.02)^3+5(-0.02)^4 +1(-0.02)^5`

`0.98^5=(1)+(-0.1)+(0.004)+(-0.00008)+0.0000008+(-0.0000000032)`

`0.98^5=0.9039207968`

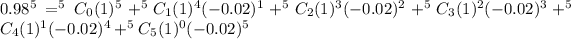
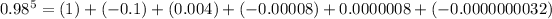
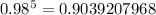
Therefore the value of
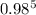`0.98^5` is 0.9039207968.