Question

Please

`\lim_(n \to \infty) ((n+1)!)/(n!-(n+1)!)`

Answer 1

Hi there!
We are given the function -

`\lim_(n \to \infty) ((n+1)!)/(n!-(n+1)!)`
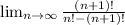
and are told to find the limit of the function.
The limit would be n approaches infinity, giving us an answer of -1.
Here is how you solve this:

`((n+1)!)/(n!-(n+1)!)`
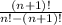
Divide by (n + 1)! -

`(1)/((1)/(n+1)-1 )`
Now, we can refine the function -

`\lim_(n \to \infty)(1)/((1)/(n+1)-1 )`
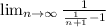
Now, just simplify. This gives us -

`\lim_(n \to \infty) (1)`
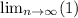
We can use the rule
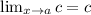
`\lim_(x \to a)c=c` to simplify the whole thing to get 1. Finally, we plug it back into our second derived equation to get 1/-1, which simplifies to -1. Therefore, the answer is -1. Hope this helped and have a great day!