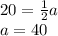Answer:
The value of a is 80
Explanation:
The distance of a point
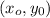 from the y-axis can be written as
from the y-axis can be written as
 because the x-coordinate of the y-axis is zero.
because the x-coordinate of the y-axis is zero.
Similarly, the distance of a point from the x-axis can be written as
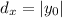
since the y-coordinate of the x-axis is zero.
In this problem:
- The distance of the point A (−30, −45) from the y-axis can be written as
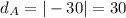
- The distance of point B (5a,2a) from the x-axis can be written as
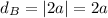
Since
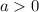
We are told that 2/3 of the distance from the y-axis to point A (−30, −45) is equal to 1/4 of the distance from the x-axis to point B(a, a), which means

Therefore,
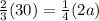
And solving for a,