Question

The length of a rectangle is 5/2 units greater than twice its width. If its width is w, which expression gives the perimeter of the rectangle in terms of w?

1. 2(5/2w) + w
2. 5/2w + w
3. 3w + 10/2
4. 6w + 5

Answer 1

Option 4 is correct

`P=5+6w`

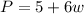
Explanation:

Perimeter of a rectangle is given by:

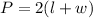`P=2(l+w)` ....[1]

where w be the width of the rectangle and l be the length of the rectangle.

As per the statement:

length of a rectangle is 5/2 units greater than twice its width.

⇒
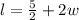`l = (5)/(2)+ 2w` units

Substitute this in [1] we get;

`P=2((5)/(2)+ 2w+w)`

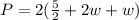
Combine like terms;

`P=2((5)/(2)+3w)`

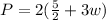
Using distributive property:
`a\cdot (b+c) =a\cdot b+ a\cdot c`

`P=5+6w`

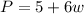
Therefore, the perimeter of the rectangle in terms of w is
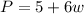`P=5+6w` units