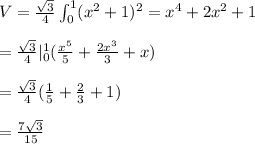Question

What is the volume of the solid whose cross-sections are equilateral triangles perpendicular to the x -axis and with bases on the region bounded by curves y = x 2 + 1 , x = 1 , and x -axis and the y -axis ?

Answer 1

The volume is the sum of all the areas of the cross-sections.

`V = \int_a^b A(x) dx`

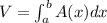
The Area is the area of an equilateral triangle, where the length of the base is distance from curve 'x^2 + 1' and x-axis.
The height of an equilateral triangle is

`(√(3))/(2) b = (√(3))/(2) (x^2 +1)`

Therefore Area of triangle is:

`A(x) = (1)/(2) b h = (√(3))/(4) (x^2 + 1)^2`

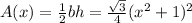
Now integrate to find Volume

`V = (√(3))/(4)\int_0^1 (x^2 + 1)^2 = x^4 +2x^2 +1 \\ \\ =(√(3))/(4)|_0^1 ((x^5)/(5) + (2x^3)/(3) + x) \\ \\ =(√(3))/(4) ((1)/(5) + (2)/(3) +1) \\ \\ = (7 √(3))/(15)`