Question

Plz Help! :)

Which ordered pairs lie on the graph of the exponential function
f(x) = 3(1/4)^x

Select each correct answer.
A.​ (−2,48) ​

B. (0,3) ​

C. (2,3/16) ​

D.​ (12,0) ​

Answer 1

B
when x=0, f(3)=3(1/4)^0
any number to the 0th power is 1, so f(3)=3*1=3
A, C are also correct. (1/4)^-2=16, (1/4)^2=1/16

Answer 2

A.​ (−2,48) ​

B. (0,3) ​

C. (2,3/16) ​

Explanation:

The given function is

`f(x)=3((1)/(4) )^(x)`

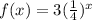
To find those ordered pairs that lie on the graph, we need to evaluate each of them

A. (−2,48) ​

`f(-2)=3((1)/(4) )^(-2)=3(4)^(2)=3(16)=48`

This pair lies on the graph.

B. (0,3)

`f(0)=3((1)/(4) )^(0)=3(1)=3`

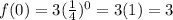
This pair lies on the graph.

C. (2,3/16) ​

`f(2)=3((1)/(4) )^(2)=3((1)/(16) )=(3)/(16)`

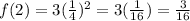
This pair also lies on the graph.

D.​ (12,0) ​

`f(12)=3((1)/(4) )^(12)=(3)/(16,777,216)`

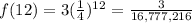
This pair doesn't lie on the graph, because it doesn't satisfy the exponential function.

Therefore, the right asnwer are A, B and C.