Question

The area of a rectangle is (x^4+4x^3+3x^2-4x-4),and the length of the rectangle is (x^3+5x^2+8x+4). if the area = length x width, what is the width of the rectangle

Answer 1

W = A/L
W = (x^4+4x^3+3x^2-4x-4) / (x^3+5x^2+8x+4)
W = x - 1

Answer 2

Answer: x-1

Step-by-step explanation: if the area of a rectangle is the length multiplied by the width, the width would be the area divided by the length:

A=L*W

W=A/L

substituting the given expressions:

`W=(x^(4)+4x^(3)+3x^(2)-4x-4   )/(x^(3) +5x^(2)+8x+4 )`

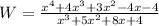
now dividing the polynomials we have that the first term of the quotient is given by:

`(x^(4) )/(x^(3) ) =x`

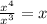
when multiplying this term by the divisor and substracting the result from the dividend we are left with the following polynomial:

`-x^(3)-5x^(2)-8x-4`

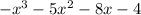
the second term of the quotient is given by:

`(-x^(3) )/(x^(3) ) =-1`

when multiplying by the divisor and substracting it from the divident the remainder is zero.

so the answer is W=x-1