Question

What are the zeros of the function? What are their multiplicities?
y=(x-2)(x+7)^3

Answer 1

(2,0) is a single
(-7,0) is a triple

Answer 2

1)
`S=\left \{ 2,-7 \right \}` 2) x=2, multiplicity 1 x=-7, multiplicity is 3.

Explanation:

1) The zeros of this function are the roots of it. Which number added to -2 will return 0 for the first factor (x-2)? Similarly, which one added to -7 for the second factor (x+7)³ will return 0?

`y=(x-2)(x+7)^3\Rightarrow (x-2)(x+7)^3=0\rightarrow (x-2)=0\\\therefore(2-2)(x+7)^(3)=0\Rightarrow 0(x+7)^(3)=0\,x'=2\\(x-2)(-7+7)^(3)=0\Rightarrow (x-2)(0)^(3)=0\.x''=-7\\S=\left \{ 2,-7 \right \}`

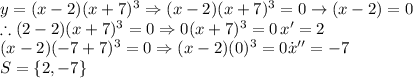
2) The multiplicity of a function is the number of repeated times, a factor of a polynomial function appears in its factored form. So,

`y=(x-2)(x+7)^3\Rightarrow y=(x-2)(x+7)(x+7)(x+7)`

The factor is (x+7) whose multiplicity is 3, then x=-7, multiplicity=3

The factor (x-2), then x=2, multiplicity =1