Question

What is the temperature of 1.25 moles of an ideal gas if it occupies 20.0 liters at a pressure of 1.45 atm?

Answer 1

Your answer is gonna be B

Answer 2

The temperature of 1.25 moles of an ideal gas if it occupies 20.0 liters at a pressure of 1.45 atm is 9.58 °C

Step-by-step explanation:

The complete question is with options, as follow:

"What is the temperature of 1.25 moles of an ideal gas if it occupies 20.0 liters at a pressure of 1.45 atm?

9.58°C

17.2°C

23.2°C

36.3°C"

An ideal gas is characterized by three state variables: absolute pressure (P), volume (V), and absolute temperature (T). The relationship between them constitutes the ideal gas law, an equation that relates the three variables as follows:

`P*V=n*R*T`

where:

• P = pressure
• V = volume
• n = number of moles
• R = gas constant, whose value depends on the units you use
• T = temperature

In this case, the values ​​you know are:

• P=1.45 atm
• V= 20 L
• n= 1.25 moles

• R= 0.08205746
  `(atm*L)/(mol*K)`

• T=?

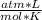
Replacing:

1.45 atm*20 L= 1.25 moles*0.08205746
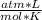`(atm*L)/(mol*K)`*T

Solving, you get:

`T=(1.45 atm*20L)/(1.25 moles*0.08205746(atm*L)/(mol*K) )`

T=282.73 °K

Being 0 ° C = 273.15 ° K, then:

T=282.73 °K=9.58 °C

The temperature of 1.25 moles of an ideal gas if it occupies 20.0 liters at a pressure of 1.45 atm is 9.58 °C