Question

In triangle ΔABC, ∠C is a right angle and CD is the height to AB , Find the angles in ΔCBD and ΔCAD if: m∠A = 20°

Answer 1

triangle CBD = 180-20-90=70
trangle CAD=20

Answer 2

The measure of angle B is 70°.

The measure of angle DCB is 20°.

The measure of angle DCA is 70°.

Explanation:

Given information: In triangle ΔABC, m∠A = 20°, ∠C is a right angle and CD is the height to AB.

It means CD⊥AB and
`\angle ACB=90^(\circ)`.

`\angle CDA=\angle CDB=90^(\circ)`

According to the angle sum property, the sum of all interior angles of a triangle is 180°.

In triangle ABC,

`\angle A+\angle B+\angle C=180`

`20+\angle B+90=180`

`\angle B+110=180`

`\angle B=180-110`

`\angle B=70`

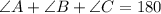
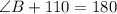
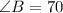
Therefore, the measure of angle B is 70°.

In triangle CBD,

`\angle CBD+\angle BDC+\angle DCB=180`

`70+90+\angle DCB=180`

`160+\angle DCB=180`

`\angle DCB=180-160`

`\angle DCB=20`

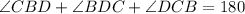
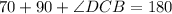
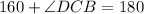
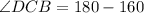
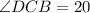
Therefore, the measure of angle DCB is 20°.

n triangle CAD,

`\angle CAD+\angle ADC+\angle DCA=180`

`20+90+\angle DCA=180`

`110+\angle DCA=180`

`\angle DCA=180-110`

`\angle DCA=70`

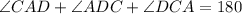
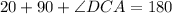
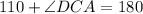
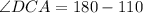
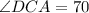
Therefore, the measure of angle DCA is 70°.