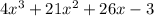Question

F(x)=x^4+7x^3+13x^2-3x-18

Answer 1

I assume for this problem you are looking for the derivative?
If so. I hope this helps!
Apply the sum difference rule > d/dx(x^4) + d/dx(7^3) + d/dx(13x^2) - d/dx(3x) - d/dx(18)
For d/dx(x^4), d/dx(7^3), d/dx(13x^2), d/dx(3x), and d/dx(18). We want to take the constant out and the apply the power rule of
`(d)/(dx) (x^a) = a * x^(a - 1)`

d/dx(x^4) >
`4x^(4 - 1) \ \textgreater \ 4x^3`

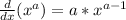
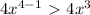
d/dx(7^3) >
`7 (d)/(dx) (x^3) \ \textgreater \ 7 * 3x^(3 - 1) \ \textgreater \ 21x^2`

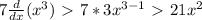
d/dx(13x^2) >
`13 (d)/(dx) (x^2) \ \textgreater \ 13 * 2x^(2 - 1) \ \textgreater \ 26x`

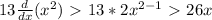
d/dx(3x) >
`3 (d)/(dx) (x) \ \textgreater \ 3 * 1 \ \textgreater \ 3`

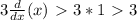
d/dx(18) >
`Deriv OFconstant \ \textgreater \ (d)/(dx)(a) = 0 \ \textgreater \ 0`

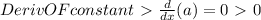
Now we can combine these all.

`4x^3 + 21x^2 + 26x - 3 - 0 \ \textgreater \ Simplify \ \textgreater \ 4x^3 + 21x^2 + 26x - 3`
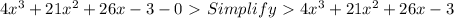
Therefore our final answer is

`4x^3 + 21x^2 + 26x - 3`