Answer:
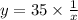
Explanation:
Given : y varies inversely with x
To Find: Write a function that models the inverse function. x = 5 when y = 7
Solution:
We are given that y varies inversely with x
So,

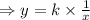 ---A
---A
where k is the constant of proportionality
Now we are given that x = 5 when y = 7
So,
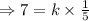

Substitute the value of k in A
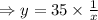
Hence a function that models the inverse function is
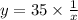 .
.