Question

Please help!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answer 1

First we want to find the LCM (Least common multiple) of 3 - x, x + 3, x^2 - 9.
Factor the expressions!
x^2 - 9 > Rewrite 9 as 3^2
x^2 - 3^2 > Now apply the difference of squares rule: x^2 - y^2 = (x + y)(x - y)
x^2 - 3^2 = (x + 3)(x - 3)
Now we want to make a a expression that is comprised of factors that appear in at least one of the factored expressions!
(-x + 3)(x + 3)(x - 3)
Multiply by LCM >
`(2)/(3 - x) (-x + 3)(x + 3)(x - 3) + (3)/(x + 3) (-x + 3)(x + 3)(x - 3)`
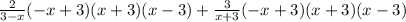
Which this equals >
`(6x)/(x^2 - 9) (-x + 3)(x + 3)(x - 3)`
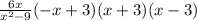
Now we want to refine the answer.
2(x + 3)(x - 3) + 3(-x + 3)(x - 3) = -6x(x - 3) < We want to solve this.
(x + 3)(x - 3) > Distribute parenthesis using..
`(a + b)(a - b) = a^2 - b^2, a = x, b = 3 \ \textgreater \ x^2 - 3^2 (3^2 = 9) \ \textgreater \ x^2 - 9`
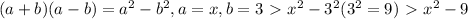
This translates to 2(x^2 - 9) which we want to expand further.
Distribute using...
`a(b + c) = ab + ac (a = 2, b = x^2, c = -9) \ \textgreater \ 2 * x^2 + 2(-9)`
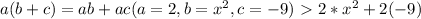
Next apply the minus - plus rule > +(-a) = -a > 2x^2 - 2 * 9 > Multiply the numbers 2 * 9 = 18 > 2x^2 - 18. > 2x^2 - 18 + 3(-x + 3)(x - 3)
Now we want to expand (-x + 3)(x - 3) > use the rule of (a + b)(c + d) = ac + ad + bc + bd where a = -x, b = 3, c = x, d = -3
-x * x - x(-3) + 3 * x + 3(-3)
Apply the minus - plus rule again.
-xx + x * 3 + 3x - 3 * 3 > Now we want to simplify this > add the similar elements 3x + 3x = 6x > -xx - 6x - 3 * 3 > Now apply the exponent rule of a^b * a^c = a^b + c > xx = x^1 + 1 = x^2 > Multiply the numbers 3 * 3 = 9 > x^2 - 6x - 9
Now we have 3(-x^2 + 6x + 9) > Distribute the parenthesis > 3(-x^2) + 3 * 6x + 3(-9)
Apply the minus - plus rule again.
-3x^2 + 3 * 6x - 3 * 9 > Simplify more > Multiply 3 by 6 to get 18 > -3x^2 + 18x - 3 * 9 > Multiply 3 by 9 > -3x^2 + 18x - 27
Combine the two.
2x^2 - 18 - 3x^2 + 18x - 27 > Simplify this further > Group the like terms > 2x^2 - 3x^2 + 18x - 18 - 27 > Add the similar elements (2x^2 - 3x^2 = -x^2)
-x^2 + 18x - 18 - 27 > Subtract the numbers -18 by -27 to get -45 > -x^2 + 18x - 45
Woo-wee! Now we have -6x(x - 3) to expand.
Distribute the parenthesis using a(b + c) = ab + ac where a = -6x, b = x, c = -3 > -6x * x - 6x(-3)
Apply the minus - plus rule again.
-6xx + 6x * 3
Now apply the exponent rule of
`a^b * a^c = a^(b + c) \ \textgreater \ xx = x^(1 + 1) = x^2 \ \textgreater \ -6x^2 + 3 * 6x`
Multiply 6 by 3 to get 18 > -6x^2 + 18x
SO now we have >
`-x^2 + 18x - 45 = -6x^2 + 18x \ \textgreater \ Subtract -6x^2 + 18 from both sides`

`-x^2 + 18x - 45 - (6x^2 + 18x) = -6x^2 + 18x - (6x^2 + 18x) \ \textgreater \ Simplify`

`5x^2 - 45 = 0`
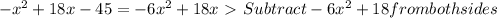
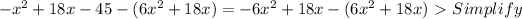
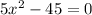
Now that we have 5x^2 - 45 = 0, we have to plug this into the quadratic equation.
-0 + sqrt0^2 - 4 * 5(-45)/2 * 5 > Apply the rule of 0^a = 0 > 0^2 = 0 > -0 + sqrt0 - 4 * 5(-45)/2 * 5
So lets take -0 + sqrt0 - 4 * 5(-45) and apply the rule -(-a) = a > sqrt0 + 4 * 5 * 45 > Multiply the numbers > sqrt0 + 900 > sqrt900 > -0 + sqrt900 = sqrt900
Now we have sqrt900/10 > Factor it >
`Apply rad rule \sqrt[n]{ab} = \sqrt[n]{a} \sqrt[n]{b} \ \textgreater \ √(2^2) √(3^2) √(5^2) \ \textgreater \ Apply \sqrt[n]{a^n} = a`
Of course assuming a is greater than or equal to zero.

`√(2^2) = 2, √(3^2) = 3, √(5^2) = 5 \ \textgreater \ 2 * 3 * 5 \ \textgreater \ Factor 10 = 2 * 5`

`(2 * 3 * 5)/(2 * 5) \ \textgreater \ Divide (2)/(2) = 1 \ \textgreater \ (3 * 5)/(5)`
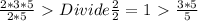
Now cancel the common factor of 5 to get 3.
Our first x value is 3 (x = 3).
Do the same thing for the next quadratic plugin except use the fraction rule for sqrt900/10 of
`(-a)/(b) = -(a)/(b) \ \textgreater \ -3`
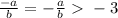
Then you want to find the undefined singularity points.
Take the denominators of
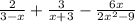
`(2)/(3 - x) + (3)/(x + 3) - (6x)/(2x^2 - 9)` and compare to zero.
3 - x = 0
Subtract 3 from both sides.
3 - x - 3 = 0 - 3 > Simplify > -x = -3
Now divide both sides by -1 > -x/-1 = -3/-1 > 3
x + 3 = 0
Subtract 3 from both sides
x + 3 - 3 = 0 - 3
x = -3
These two points are undefined, therefore our problem has no solution!
Also if you were wondering about the last denom, plug it into the quadratic equation again and you will get x = 3, x = -3.
The points that are undefined are (x = 3, x = -3).

Answer 2

The value of x in the given equation is determined as - 3. (Option A).

How to calculate the value of x?

The value of x in the given equation is calculated by applying the following formula as shown below;

`(2)/(3 - x) + (3)/(x + 3) = (6x)/(x^2 - 9)`

The given equation is simplified as follows;

`(2)/(3 - x) + (3)/(x + 3) = (6x)/((x + 3)(x - 3))`

`(2(x + 3) + 3(3 - x))/((3 - x)(x + 3)) = (6x)/((x + 3)(x - 3))\\\\(2x + 6 + 9 - 3x)/((3 - x)(x + 3)) = (6x)/((x + 3)(x - 3)) \\\\(15 - x)/((3 - x)(x + 3)) = (6x)/((x + 3)( x - 3))`

Cross and multiply, to simplify the equation further;

6x(3 - x)(x + 3) = (15 - x)(x + 3)(x - 3)

6x[ 3x + 9 - x² - 3x ] = (15 - x) [x² - 9]

6x (9 - x²) = (15 - x)(x² - 9)

-6x(x² - 9) = (15 - x)(x² - 9)

-6x = 15 - x

-6x + x = 15

-5x = 15

x = -15 / 5

x = - 3

Thus, the value of x in the given equation is determined as - 3.